Riesz space

In mathematics a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space where the order structure is a lattice.

Riesz spaces are named after Frigyes Riesz who first defined them in his 1928 paper Sur la décomposition des opérations fonctionelles linéaires.

Riesz spaces have wide ranging applications. They are important in measure theory, in that important results are special cases of results for Riesz Spaces. E.g. the Radon-Nikodym theorem follows as a special case of the Freudenthal spectral theorem. Riesz spaces have also seen application in Mathematical economics through the work of Greek-American economist and mathematician Charalambos D. Aliprantis.

1 Definition
2 Basic properties
3 Order convergence
4 Subspaces
5 Projection properties
6 Examples
7 Properties
8 References

Definition

A Riesz space E is defined to be a vector space endowed with a compatible ordered lattice structure. Specifically, every finite subset of E has a supremum and infimum.

Basic properties

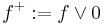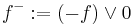Every element f in E has unique positive and negative parts, written $f^%2B:=f\vee 0$ and $f^-:=(-f)\vee 0$ . Then it can be shown that, 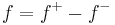$f=f^%2B-f^-$ and an absolute value can be defined by 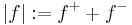$|f|:=f^%2B%2Bf^-$ . Every Riesz space is a distributive lattice and has the Riesz decomposition property

Order convergence

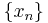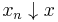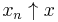There are a number of meaningful non-equivalent ways to define convergence of sequences or nets with respect to the order structure of a Riesz space. A sequence $\{x_n\}$ in a Riesz space E is said to converge monotonely if it is a monotone decreasing (increasing) sequence and its infimum (supremum) x exists in E and denoted $x_n\downarrow x$ ( $x_n\uparrow x$ ).

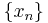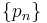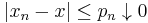A sequence $\{x_n\}$ in a Riesz space E is said to converge in order to x if there exists a monotone converging sequence $\{p_n\}$ in E such that $|x_n-x|\leq p_n\downarrow 0$ .

If u is a positive element a Riesz space E then a sequence 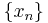$\{x_n\}$ in E is said to converge u-uniformly to x for any 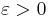$\varepsilon >0$ there exists an N such that 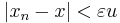$|x_n-x|<\varepsilon u$ for all n>N.

Subspaces

Being vector spaces, it is also interesting to consider subspaces of Riesz spaces. The extra structure provided by these spaces provide for distinct kinds of Riesz subspaces. The collection of each kind structure in a Riesz space (e.g. the collection of all Ideals) forms a distributive lattice.

Ideals

A vector subspace I of a Riesz space E is called an ideal if it is solid, meaning if for any element f in I and any g in E, |g| ≤ |f| implies that g is actually in I. The intersection of an arbitrary collection of ideals is again an ideal, which allows for the definition of a smallest ideal containing some non-empty subset A of E, and is called the ideal generated by A. An Ideal generated by a singleton is called a principle ideal.

Bands and $\sigma$ -Ideals

A band B in a Riesz space E is defined to be an ideal with the extra property, that for any element f in E for which its absolute value |f| is the supremum of an arbitrary subset of positive elements in B, that f is actually in B. $\sigma$ -Ideals are defined similarly, with the words 'arbitrary subset' replaced with 'countable subset'. Clearly every band is a $\sigma$ -ideal, but the converse is not true in general.

As with ideals, for every non-empty subset A of E, there exists a smallest band containing that subset, called the band generated by A. A band generated by a singleton is called a principle band.

Disjoint complements

Two elements f,g in a Riesz space E, are said to be disjoint, written 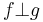$f\bot g$ , when 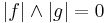$|f|\wedge |g|=0$ . For any subset A of E, its disjoint complement 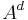$A^d$ is defined as the set of all elements in E, that are disjoint to all elements in A. Disjoint complements are always bands, but the converse is not true in general.

Projection bands

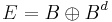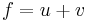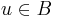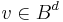A band B in a Riesz space, is called a projection band, if $E=B\oplus B^d$ , meaning every element f in E, can be written uniquely as a sum of two elements, $f=u%2Bv$ , with $u\in B$ and $v\in B^d$ . There then also exists a positive linear idempotent, or projection, 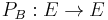$P_B:E\to E$ , such that $P_B(f)=u$ .

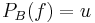The collection of all projection bands in a Riesz space forms a Boolean algebra. Some spaces do not have non-trivial projection bands (e.g. $C([0,1])$ ), so this Boolean algebra may be trivial.

Projection properties

There are numerous projection properties that Riesz spaces may have. A Riesz space is said to have the (principle) projection property if every (principle) band is a projection band.

The so-called main inclusion theorem relates these properties. Super Dedekind completeness implies Dedekind completeness; Dedekind completeness implies both Dedekind $\sigma$ -completeness and the projection property; Both both Dedekind $\sigma$ -completeness and the projection property separately imply the principle projection property; and the principle projection property implies the Archimedean property.

None of the reverse implications hold, but Dedekind $\sigma$ -completeness and the projection property together imply Dedekind completeness.

Examples

The space of continuous real valued function on a set X with compact support with the pointwise partial order defined by f ≤ g when f(x) ≤ g(x) for all x in X, is a Riesz space.

Properties

Riesz spaces are lattice ordered groups
Every Riesz space is a distributive lattice

References

Bourbaki, Nicolas; Elements of Mathematics: Integration. Chapters 1–6; ISBN 3-540-41129-1
Riesz, Frigyes; Sur la décomposition des opérations fonctionelles linéaires , Atti congress. internaz. mathematici (Bologna, 1928) , 3 , Zanichelli (1930) pp. 143–148
Sobolev, V. I. (2001), "Riesz space", Encyclopædia of Mathematics, Springer, ISBN 978-1-4020-0609-8, http://eom.springer.de/R/r082290.htm
Zaanen, Adriaan C. (1996), Introduction to Operator Theory in Riesz spaces, Springer, ISBN 3-540-61989-5

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›